What Does It Mean To Normalize Data

What if your data is NOT Normal?

In this article, we discuss the Chebyshev's bound for statistical data analysis. In the absence of whatever thought about the Normality of a given data set, this leap tin can be used to gauge the concentration of data around the mean.

Introduction

This is Halloween week, and in between the tricks and treats, we, data geeks, are chuckling over this cute meme over the social media.

You lot remember this is a joke? Let me tell you, this is not a laughing thing. It is scary, true to the spirit of Halloween!

If nosotros cannot presume that most of our data (of business, social, economic, or scientific origin) are at least approximately 'Normal' (i.due east. they are generated by a Gaussian procedure or past a sum of multiple such processes), then we are doomed!

Here is an extremely brief list of things that will not be valid,

The whole concept of six-sigma
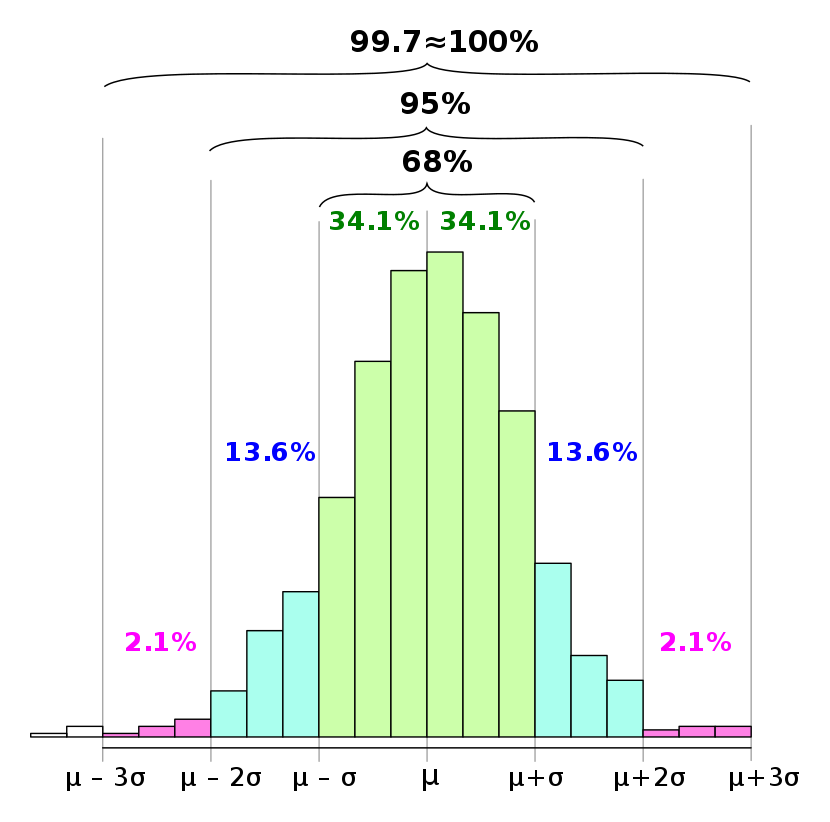
The famous 68–95–99.7 rule
The 'holy' concept of p=0.05 (comes from ii sigma interval) in statistical assay

Scary enough? Allow'south talk more about it…

The Omnipotent and Omnipresent Normal Distribution

Allow'due south keep this section brusque and sweet.

Normal (Gaussian) distribution is the most widely known probability distribution. Hither are some links to the manufactures describing its power and wide applicability,

Why Data Scientists love Gaussian

How to Dominate the Statistics Portion of Your Information Scientific discipline Interview
What's So Important about the Normal Distribution?

Because of its appearance in various domains and the Central Limit Theorem (CLT), this distribution occupies a central place in data science and analytics.

So, what's the problem?

This is all hunky-dory, what is the upshot?

The outcome is that often you may notice a distribution for your specific data set, which may not satisfy Normality i.e. the properties of a Normal distribution. But considering of the over-dependence on the supposition of Normality, most of the business analytics frameworks are tailor-fabricated for working with Normally distributed information sets.

Information technology is near ingrained in our subconscious mind.

Let's say you are asked to discover check if a new batch of data from some process (engineering or business) makes sense. By 'making sense', you mean if the new data belong i.e. if it is within 'expected range'.

What is this 'expectation'? How to quantify the range?

Automatically, as if directed by a subconscious drive, we measure out the mean and the standard deviation of the sample dataset and proceed to cheque if the new information falls within certain standard deviations range.

If nosotros take to piece of work with a 95% conviction leap, then we are happy to see the data falling inside 2 standard deviations. If nosotros need stricter bound, we check 3 or four standard deviations. We calculate Cpk, or nosotros follow six-sigma guidelines for ppm (parts-per-million) level of quality.

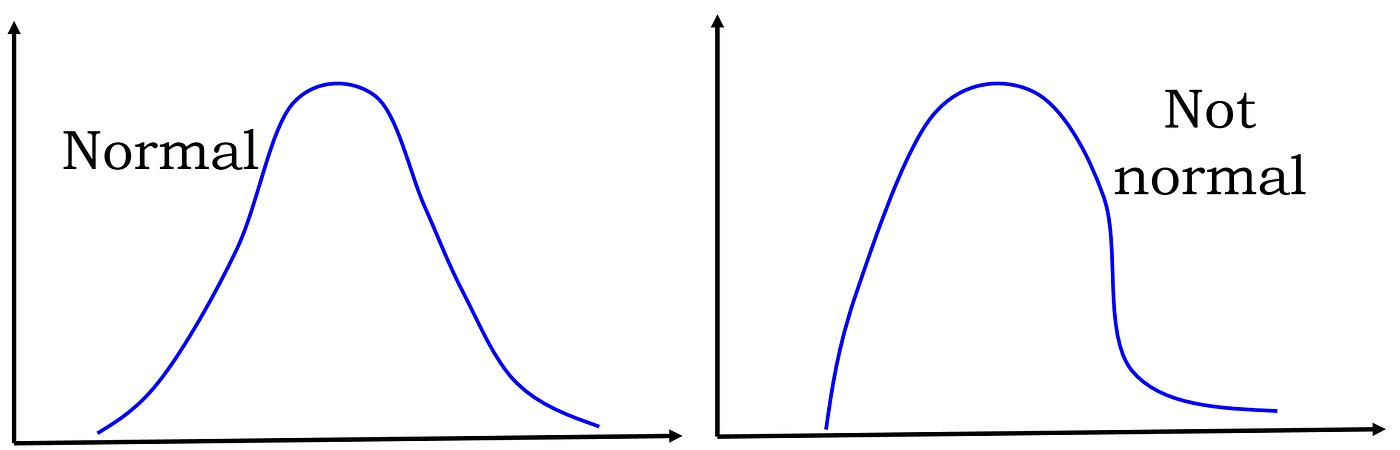
All these calculations are based on the implicit assumption that the population data (Not the sample) follows Gaussian distribution i.e. the fundamental procedure, from which all the information has been generated (in the past and at the nowadays), is governed by the pattern on the left side.

But what happens if the data follows the blueprint on the right side?

Or, this, and… that?

Is there a more universal bound when the information is NOT Normal?

At the end of the day, we will even so need a mathematically sound technique to quantify our confidence bound, fifty-fifty if the data is not normal. That means, our adding may modify a footling, but we should still exist able to say something like this-

"The probability of observing a new data betoken at a certain distance from the average is such and such…"

Manifestly, we need to seek a more universal jump than the cherished Gaussian bounds of 68–95–99.7 (corresponding to 1/two/iii standard deviations distance from the mean).

Fortunately, in that location is one such bound called "Chebyshev Bound".

What is Chebyshev Jump and how is information technology useful?

Chebyshev's inequality (also called the Bienaymé-Chebyshev inequality) guarantees that, for a wide grade of probability distributions, no more than a sure fraction of values tin be more a certain altitude from the hateful.

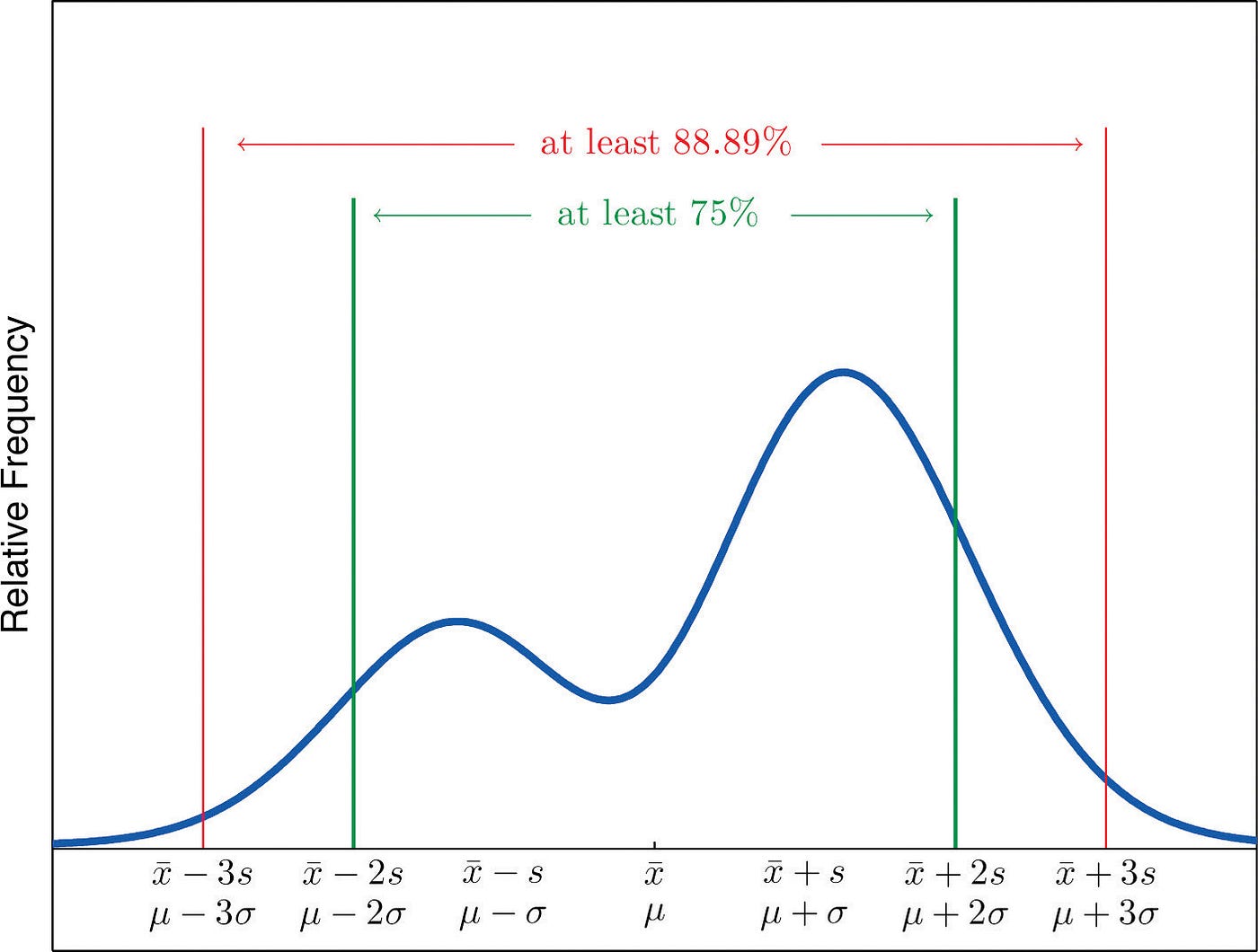
Specifically, no more than 1/k² of the distribution's values can exist more than k standard deviations away from the mean (or equivalently, at to the lowest degree 1−1/k² of the distribution's values are within k standard deviations of the mean).

It applies to nearly unlimited types of probability distributions and works on a much more relaxed assumption than Normality.

How does it piece of work?

Even if you don't know anything about the secret process backside your data, there is a expert chance you lot can say the post-obit,

"I am confident that 75% of all data should fall within 2 standard deviations abroad from the hateful",

Or,

I am confident that 89% of all data should fall within 3 standard deviations away from the hateful".

Hither is what it looks similar for an arbitrary looking distribution,

Image Credit: https://2012books.lardbucket.org/books/commencement-statistics/s06-05-the-empirical-rule-and-chebysh.html

How to apply it?

As you can approximate by now, the basic mechanics of your data analysis does not demand to modify a bit. You will still assemble a sample of the data (larger the ameliorate), compute the aforementioned two quantities that you are used to calculating — mean and standard divergence, and so apply the new bounds instead of 68–95–99.vii rule.

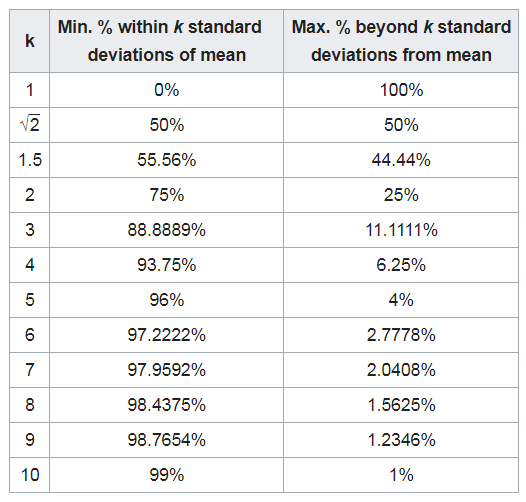
The table looks like post-obit (here k denotes that many standard deviations away from the mean),

Image: https://en.wikipedia.org/wiki/Chebyshev%27s_inequality

A video demo of its awarding is here,

What's the grab? Why don't people use this 'more universal' bound?

It is obvious what the take hold of is by looking at the tabular array or the mathematical definition. The Chebyshev dominion is much weaker than the Gaussian rule in the affair of putting bounds on the information.

Information technology follows a 1/k² pattern as compared to an exponentially falling design for the Normal distribution.

For example, to leap anything with 95% conviction, you need to include data upward to 4.5 standard deviations vs. only 2 standard deviations (for Normal).

But it can all the same save the day when the data looks nil like a Normal distribution.

Is in that location anything improve?

There is another bound called, "Chernoff Leap"/Hoeffding inequality which gives an exponentially sharp tail distribution (as compared to the 1/k²) for sums of independent random variables.

This tin can too be used in lieu of the Gaussian distribution when the data does not await Normal, simply only when we have a high degree of confidence that the underlying process is composed of sub-processes which are completely independent of each other.

Unfortunately, in many social and concern cases, the final data is the result of an extremely complicated interaction of many sub-processes which may have strong inter-dependency.

Summary

In this article, we learned about a particular blazon of statistical bound which can exist applied to the widest possible distribution of data independent of the assumption of Normality. This comes handy when we know very petty about the true source of the information and cannot assume information technology follows a Gaussian distribution. The leap follows a power law instead of an exponential nature (similar Gaussian) and therefore is weaker. But it is an important tool to have in your repertoire for analyzing any arbitrary kind of data distribution.